背景
Steffen Rendle于2012年提出FM模型,旨在解决稀疏矩阵下的特征组合问题。传统机器学习问题,一般仅考虑如何对特征赋予权重,而没有考虑特征间存在相互作用,FM模型的提出较好地解决了该问题。
相比于SVM的优势
- 对于稀疏数据有更强的学习能力
- 线性时间复杂度,不依赖于支撑向量
应用
- 回归问题
- 二分类问题
- 排序
原理
传统线性回归模型
我们用广告的CTR(点击率)预估问题引出FM模型:根据用户和广告位等相关特征,预测用户是否点击广告。源数据如下
| Clicked? | Country | Day | Ad_type |
|---|---|---|---|
| 1 | USA | 26/11/15 | Movie |
| 0 | China | 1/7/14 | Game |
| 1 | China | 19/2/15 | Game |
由于三种特征Country、Day、Ad_type都是categorical类型的,进行ctr预估的时候往往需要经过独热编码(One-Hot Encoding)转换成数值型特征。
| Clicked? | Country=USA | Country=China | Day=26/11/15 | Day=1/7/14 | Day=19/2/15 | Ad_type=Movie | Ad_type=Game |
|---|---|---|---|---|---|---|---|
| 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 |
再利用传统的线性回归模型:
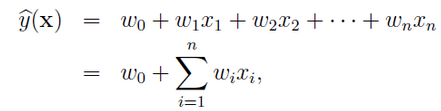
根据训练集训练出模型的参数,进行预测。
该方法存在的问题:
- 经过One-Hot编码之后,大部分样本数据特征是比较稀疏的,上面的样例中,每个样本有7维特征,但平均仅有3维特征具有非零值。而且在实际情况中,one-hot编码后的特征空间维度很大。
- 更重要的是,通过One-Hot编码方式输入到传统线性模型中进行训练,各特征分量$x_i$和$x_j$是相互独立的,但在实际应用中,通过观察大量的样本数据可以发现,某些特征经过关联之后,与label之间的相关性就会提高。例如,“USA”与“Thanksgiving”、“China”与“Chinese New Year”这样的关联特征,对用户的点击就极有可能有着正向的影响。
FM模型
由于上述问题,所以引入两个(设置多个)特征之间的组合十分有意义:
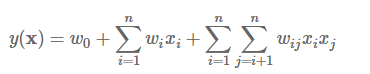
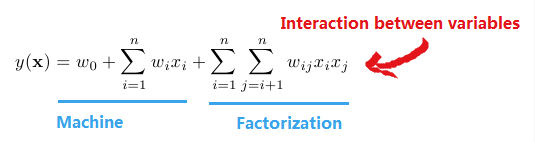
前半部分就是传统的线性模型,后半部分引入两个特征之间的关联特征。
从上面公式可以看出,组合特征的参数一共有n(n−1)/2个, 任意两个参数都是独立的。但是二次项参数训练很困难,因为:数据稀疏性普遍存在于实际应用场景中,而每个参数$w_{ij}$的训练需要大量 $x_i$和 $x_j$ 都非零的样本,训练样本的不足,很容易导致参数 $x_i$ 和$x_j$训练 不准确,最终将严重影响模型的性能。
那么,如何解决二次项参数的训练问题呢?矩阵分解提供了一种解决思路。
参考在model-based的协同过滤中的做法:一个rating矩阵可以分解为user矩阵和item矩阵,每个user和item都可以采用一个隐向量表示
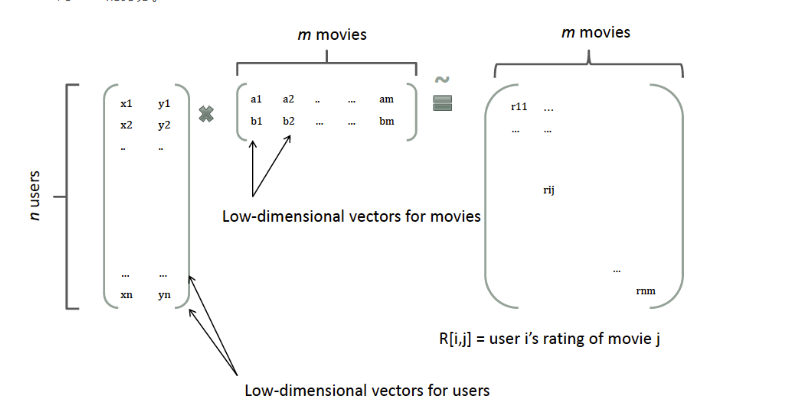
FM模型中二次项系数构成的矩阵是对称正定的,故可以用上面的分解方式分解成两个低维的矩阵相乘,即$W={V^T}V$,从而解决数据稀疏导致训练不准确的问题。至此,FM模型可以化为如下形式:
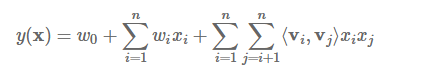
总结起来一句话就是:FM引入二维组合特征,然后利用矩阵分解降维减少了训练参数,从而能够适应数据的稀疏性。
具体解释参考美团技术团队关于FM的介绍需要的时候可以细看

FM模型复杂度
求解复杂度
模型参数已经训练出来,将新的数据输入模型求解: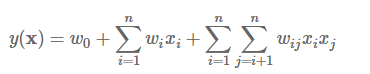
时间复杂度为$O(kn^2)$
但是如果我们依据公式$ab+ac+bc+\cdots=\frac{(a+b+c+\cdots)^2-(a^2+b^2+c^2+\cdots)}{2}$化简交叉项,具体过程如下: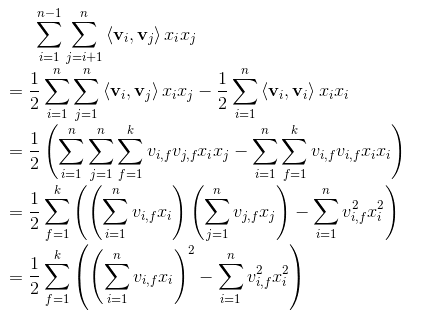
此时时间复杂度简化为$O(kn)$。由此可见,FM可以在线性时间对新样本作出预测。
模型训练复杂度
- 多元统计回归问题
- 训练方法:SGD(随机梯度下降法)
记FM模型参数为$\Theta={(w_0,w_1,w_2,\cdots,w_n,v_11,v_12,\cdots,v_nk)}^T$,共有$1+n+kn$个参数,模型各个参数的梯度如下:
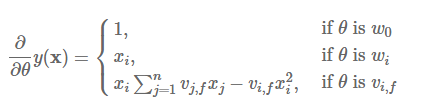

详细推导过程参考peghoty的博客
时间复杂度为$O(kn)$
开源代码库
libFM