题目

思路
- 对于二叉排序树的任何一个节点,其左子树的元素都小于右子树的元素
- 满二叉排序树树,树的结构可以确定
如果树的深度是$k$,满二叉树有$2^k-1$个元素,按从小到大的顺序排列为:$[a_1,a_2,…,a_{2^k-1}]$,则该满二叉树的结构如下:
- 根节点的元素为$a_{\frac{2^k}{2}}$,$[a_1,a_2,…,a_{\frac{2^k}{2}-1}]$中的元素在根节点的左子树中,$[a_{\frac{2^k}{2}+1},…,a_{2^k-1}]$中的元素在根节点的右子树中
- 对左子树、右子树两个区间再分别做1中的操作,得到最终的二叉排序树
给定三个节点,根据二叉排序树的性质,可以知道包含这三个节点的最小子树的根节点的值,一定在这三个节点值构成的区间$[min,max]$内
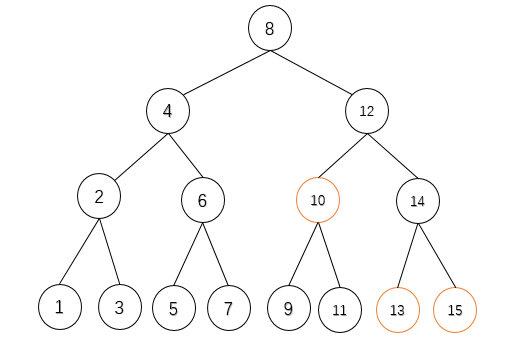
所以我们可以从上至下遍历二叉排序树
- 如果根节点root值包含在三个节点值构成的最大区间内,则根节root点就是所求
- 如果根节点值小于min,则令右子树的根节点为root
- 如果根节点值大于min,则对左子树的根节点为root
重复上述操作,直到找到一个节点值为$t$,$t\in[min,max]$,该节点即为所求
代码
|