感谢@MoreWindows的白话经典算法系列,浅显易懂,让我终于看懂了快速排序,总结一下
思想
步骤:
- 从数列中选择一个作为基准数
- 分区操作:把比基准数小的都排在基准数的左边,比基准数大的都排在基准数的右边
- 对基准数的左边和右边分治排序
具体实现:挖坑填数+分治法
这里结合个实际例子说明

根据上面的步骤,选取第一个作为基准数,接下来我们需要把比它小的数字放到它的左边,比它大的数字放到它的右边,这里就需要重点注意挖坑填数的方法了,划重点!!!
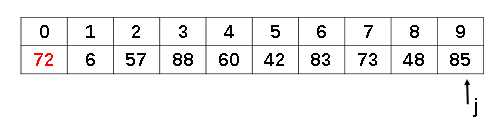 temp=72
temp=72
我们先把基准数72保存到变量temp中,这时候就相当于在数组的第一个位置上挖了一个“坑”,如果我们在后边发现有比temp小的数字,就可以把那个比较小的数字填到这个空缺的“坑”里了。
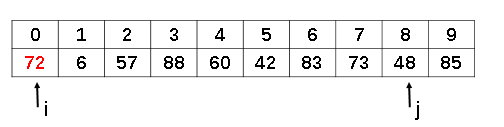
我们定义一个从后向前遍历的指针j,发现a[8]位置上的48比72小,所以我们要把48放到前面去,填补之前72留下的空缺.
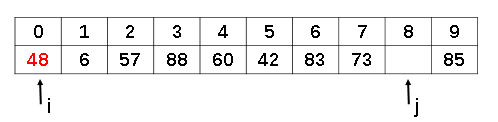
这时候原来存放48的这个位置就空了出来,有了一个新的“坑”,此时指针i向后遍历,如果找到比temp大的数字,便可以填补之前的48留下的坑了。恩,我们找到了a[3]位置上的88,将他填补到之前48留下来的“坑”里。
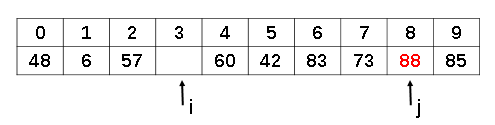
接下来继续重复上面的过程,先从后向前找到比基准值小的,填补在前面的“坑”里,然后再从前向后找比基准值大的,填补刚才空出来的“坑”。直到最终两个指着相遇。
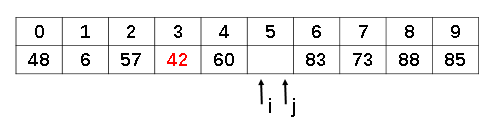
而此时空缺的位置,恰好就是基准值temp的位置。将基准值填入空缺位置,至此就完成了一次分区的操作,此时基准数前面的数字都比基准数小,后面的都比基准数大。
接下来就是对基准数前后两段数组分而治之,采用递归调用的思想,将整个数组调整至有序状态。
代码
|
时间复杂度
- 最坏时间复杂度:$O(n^2)$
- 期望时间复杂度:$O(n\log(n))$